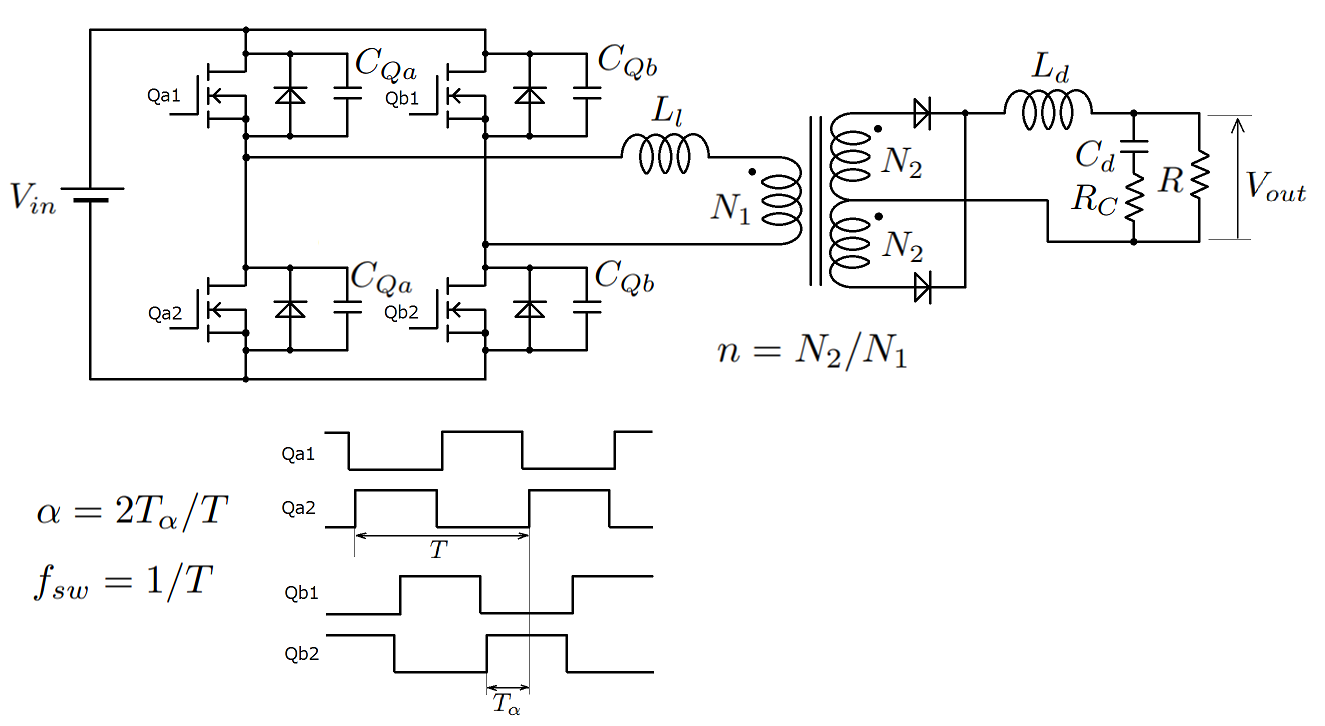
| 位相シフト率$\alpha$ | |
| インダクタ電流平均値 | A |
| インダクタ電流最大値 | A |
| インダクタ電流リプル両振幅 | Ap-p |
| インダクタ電流リプル率 | |
| コンデンサリプル電流両振幅 | Ap-p |
| コンデンサリプル電流実効値 | A |
| 出力電圧リプル両振幅 | Vp-p |
| 出力電圧リプル率 |
|
\[
\frac{\mathit{\Delta}\overline{v_{out}}(s)}{\mathit{\Delta}\alpha(s)}=\frac{b_1s+b_0}{a_2s^2+a_1s+a_0}
\]
$a_0=$ $a_1=$ $a_2=$ $b_0=$ $b_1=$ |
極 $p_1=$ $f_{p_1}=$ $\mathrm{Hz}$ $p_2=$ $f_{p_2}=$ $\mathrm{Hz}$ 零点 $z=$ $f_{z}=$ $\mathrm{Hz}$ |
| 共振用インダクタ | Wb |
| 平滑インダクタ | Wb |
| トランス 一次巻線 | Wb |
| トランス 二次巻線 | Wb |